Find the Height of a Binary Tree

Just like we find the length of a list or the number of items in a python dictionary, we can find the height of a binary tree. In this article, we will formulate an algorithm to find the height of a binary tree. We will also implement the algorithm in python and execute on a given binary tree.

What is the height of a binary tree?

Height of a binary tree is defined as the maximum distance from the root node at which a node is present in the binary tree. The height of a binary tree depends on the number of nodes and their position in the tree. If a tree has an ‘n’ number of nodes, it can have a height anywhere between log(n) + 1 to n.  The binary tree will have a height n if the tree is entirely skewed to either left or right. It will have a height of log(n)+1 if the nodes in the tree are properly distributed and the tree is a complete binary tree.

For example, the following binary tree has 7 elements.A binary tree with 7 elements can have any height between log(7)+ 1 that is 3 and 7. In our example, the nodes of the tree are properly distributed and the tree is completely balanced. Therefore, the height of the tree is 3.

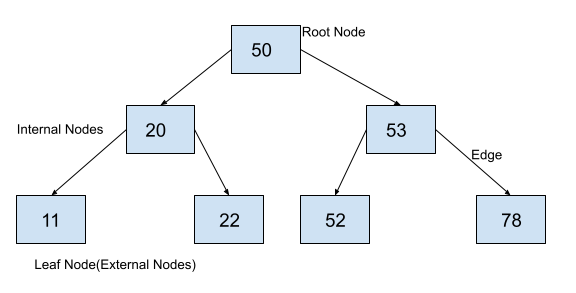
How to calculate the height of a binary tree?

To calculate the height of a binary tree, we can calculate the heights of left and right subtrees. The maximum of the height of the subtrees can be used to find the height of the tree by adding one to it. For an empty root, we can say that the height of the tree  is zero. Similarly, height of a single node will be considered as 1. 

Algorithm to find the height of a binary tree

Now that we have found a way to find the height of the binary tree, we will formulate the algorithm for finding the height as follows.

1. If we find an empty root node, we will say that the height of the tree is 0.
2. Otherwise, we will find the height of the left subtree and right subtree recursively.
3. After finding the height of the left subtree and right subtree, we will calculate their maximum height.
4. We will add 1 to the maximum height. That will be the height of the binary tree.

Implementation of the algorithm in Python

Now that we have understood and formulated the algorithm, we will implement it in Python.

from queue import Queue


class BinaryTreeNode:
    def __init__(self, data):
        self.data = data
        self.leftChild = None
        self.rightChild = None


def height(root):
    if root is None:
        return 0
    leftHeight=height(root.leftChild)
    rightHeight=height(root.rightChild)
    max_height= leftHeight
    if rightHeight>max_height:
        max_height = rightHeight
    return max_height+1


def insert(root, newValue):
    # if binary search tree is empty, create a new node and declare it as root
    if root is None:
        root = BinaryTreeNode(newValue)
        return root
    # if newValue is less than value of data in root, add it to left subtree and proceed recursively
    if newValue < root.data:
        root.leftChild = insert(root.leftChild, newValue)
    else:
        # if newValue is greater than value of data in root, add it to right subtree and proceed recursively
        root.rightChild = insert(root.rightChild, newValue)
    return root


root = insert(None, 50)
insert(root, 20)
insert(root, 53)
insert(root, 11)
insert(root, 22)
insert(root, 52)
insert(root, 78)
print("Height of the binary tree is:")
print(height(root))

Output:

Height of the binary tree is:
3

Here, we have created a binary tree node. Then, we defined functions to insert elements to the binary tree. Finally, we implemented the algorithm to find the height of a binary tree in Python.

Conclusion

In this article, we have implemented an algorithm to find the height of a binary tree. To learn more about  other data structures, you can read this article on Linked List in Python. Stay tuned for more articles on implementation of different algorithms in Python.