Graph in Python

Graphs are one of the most important data structures. Graphs are used to represent telephone networks, maps, social network connections, etc. In this article we will discuss what a graph is and how we can implement a graph in Python.

What is a graph?

In mathematics, A graph is defined as a set of vertices and edges where vertices are particular objects and edges represent the connections between the vertices. The vertices and edges are represented by using sets. 

Mathematically, a graph G can be represented as G= (V , E), where V is the set of vertices and E is the set of edges.

If an edge E_i connects vertices v1 and v2, we can represent the edge as E_i= (v1, v2).

How to represent a graph?

We will use the graph given in the following figure to learn how to represent a graph.

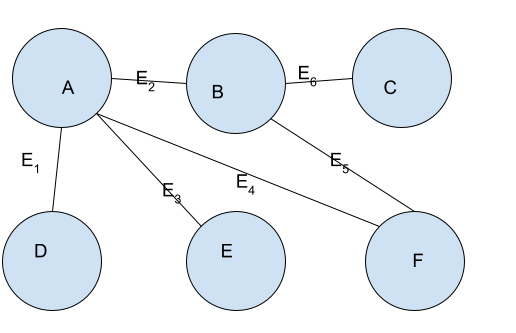
To represent a graph, we will have to find the set of vertices and edges in the graph. 

First, we will find the set of vertices. For this, we can create a set using the vertices given in the above figure. In the figure, the vertices have been named A,B,C,D,E, and F. So the set of vertices can be created as V={A, B, C, D, E, F}. 

To find the set of edges, first we will find all the edges in the graph. You can observe that there are 6 edges in the graph numbered from E₁ to E₆. An edge E_i can be created as a tuple (v1, v2) where v1 and v2 are the vertices being connected by E_i. For the above graph, We can represent the edges as follows.

• E₁=(A, D) 
• E₂ = (A,B)
• E₃= (A,E)
• E₄=(A, F)
• E₅=(B,F)
• E₆= (B,C)

The set of edges E can be represented as E= {E₁, E₂ , E₃, E₄, E₅, E₆}.

Finally, the graph G can be represented as G= (V,E) where V and E are sets of vertices and edges.

Till now, we have discussed how to represent a graph mathematically. Can you think of a way to represent a graph in a python program? Let us look into it.

How to represent a graph in Python?

We can represent a graph using an adjacency list. An adjacency list can be thought of as a list in which each vertex stores a list of all the vertices connected to it. 

We will implement the adjacency list representation of the graph in python using a dictionary and lists. 

First, we will create a python dictionary with all the vertex names as keys and an empty list (adjacency list) as their associated values using the given set of vertices.

After that, we will use the given set of edges to complete the adjacency list of each vertex that has been represented using the keys of the dictionary. For every edge (v1,v2), we will add v1 to the adjacency list of v2 and v2 to the adjacency list of v1. 

In this way, every key (vertex) in the dictionary will have an associated value (a list of vertices) and the dictionary will represent the whole graph in python. 

Given the set of vertices and edges, we can implement a graph in python as follows.

vertices = {"A", "B", "C", "D", "E", "F"}
edges = {("A", "D"), ("A", "B"), ("A", "E"), ("A", "F"), ("B", "F"), ("B", "C")}
graph = dict()
for vertex in vertices:
    graph[vertex] = []
for edge in edges:
    v1 = edge[0]
    v2 = edge[1]
    graph[v1].append(v2)
    graph[v2].append(v1)
print("The given set of vertices is:", vertices)
print("The given set of edges is:", edges)
print("Graph representation in python is:")
print(graph)

Output:

The given set of vertices is: {'F', 'D', 'B', 'E', 'A', 'C'}
The given set of edges is: {('A', 'F'), ('A', 'B'), ('B', 'C'), ('A', 'D'), ('A', 'E'), ('B', 'F')}
Graph representation in python is:
{'F': ['A', 'B'], 'D': ['A'], 'B': ['A', 'C', 'F'], 'E': ['A'], 'A': ['F', 'B', 'D', 'E'], 'C': ['B']}

In the above output, you can verify that each key of the graph has a list of vertices that are connected to it as its value.

Conclusion

In this article, we have discussed graph data structure. We also discussed the mathematical representation of a graph and how we can implement it in python. To learn more about data structures in Python, you can read this article on Linked list in python.